Research

Y. Li, H. A. Fertig, B. Seradjeh, Phys. Rev. Res.  2, 043275 (2020);
F. Nur Ünal, B. Seradjeh, A. Eckardt, Phys. Rev. Lett.  122, 253601 (2019);
M. Rodriguez-Vega, A. Kumar, B. Seradjeh, Phys. Rev. B  100, 085138 (2019);
M. Rodriguez-Vega and Babak Seradjeh, Phys. Rev. Lett.  121, 036402 (2018);
A. Kundu, H.A. Fertig, and B. Seradjeh, Phys. Rev. Lett.  116, 016802 (2016);
A. Kundu, H.A. Fertig, B. Seradjeh, Phys. Rev. Lett.  113, 236803 (2014);
Y. Li, A. Kundu, F. Zhong, and B. Seradjeh, Phys. Rev. B  90, 121401(R) (2014);
A. Kundu and B. Seradjeh, Phys. Rev. Lett.  111, 136402 (2013).

For a time-periodic Hamiltonian, although energy is not conserved, there is a conserved quasienergy, \(\varepsilon\). This conservation is a consequence of the discrete time-translation symmetry of the Hamiltonian \(H(t)\) with period \(T\), \(H(t)=H(t+T)\). As a result of this periodicity, the solutions to the Schördinger equation can be written, using Floquet's theorem, as \(e^{-i\varepsilon t/\hbar}\phi(t)\) with a periodic part \(\phi(t) = \phi(t+T)\). The quasienergy \(\varepsilon\) and Floquet wavefunction \(\phi(t)\) are the eigenvalue and eigenstate of the Floquet Hamiltonian \(H_F = H(t)-i\hbar\frac{\partial}{\partial t}\). Quasienergies that differ by an integer multiple of \(\hbar\Omega\), where \(\Omega=2\pi/T\) is the drive frequency, refer to the same physical state. Thus, they can be chosen to be in a “Floquet zone,” e.g. \(-\frac12\hbar\Omega< \varepsilon \leq \frac12\hbar\Omega\). Due to this periodic temporal structure, the quasienergy bands can be quite different in character from the static energy bands. Indeed, under certain conditions, the driven systems has steady topological bound states with no corresponding stationary bound states in a static system. This is reminiscent of “period doubling,” an effect familiar from parametric resonance and stabilization in classical systems: In addition to \(\varepsilon = 0\), steady topological bound states exist with quasienergy \(\varepsilon = \frac12\hbar\Omega\). These period-doubled states have no counterpart in the static systems. Thus, Floquet topological phases constitute an entirely new class of topological phases.

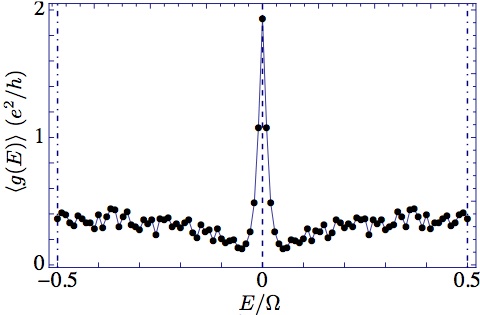
The Floquet sum rule in a disordered system.

In our first work on this topic, we showed, both analytically and numerically, Floquet Majorana fermions at quasienergy \(\varepsilon_M=0\) and/or \(\frac12\hbar\Omega\) give rise to a quantized “Floquet sum rule,” \(g(\varepsilon_M) = 2e^2/h\). Here, \(e\) is the electron's charge, \(g(\varepsilon) = \sum_{n\in\mathbb{Z}} \sigma(\varepsilon + n\hbar\Omega)\), and \(\sigma(E)\) is the usual conductance at bias \(E\). This is a natural extension of the well-known zero-bias conductance of static Majorana fermions to periodic systems. This result can be understood intuitively as the consequence of the unitarity of the interaction with the periodic drive: The sum (over \(n\)) of all transmission probabilities for processes in which scattering states exchange \(n\) “photons” with the drive is one. We showed this result is robust against disorder. Indeed, since disorder localizes the other, non-topological, states of the system, it suppresses the background peaks of \(g\) and can be used as a “sieve” to identify the Floquet Majorana fermions uniquely.

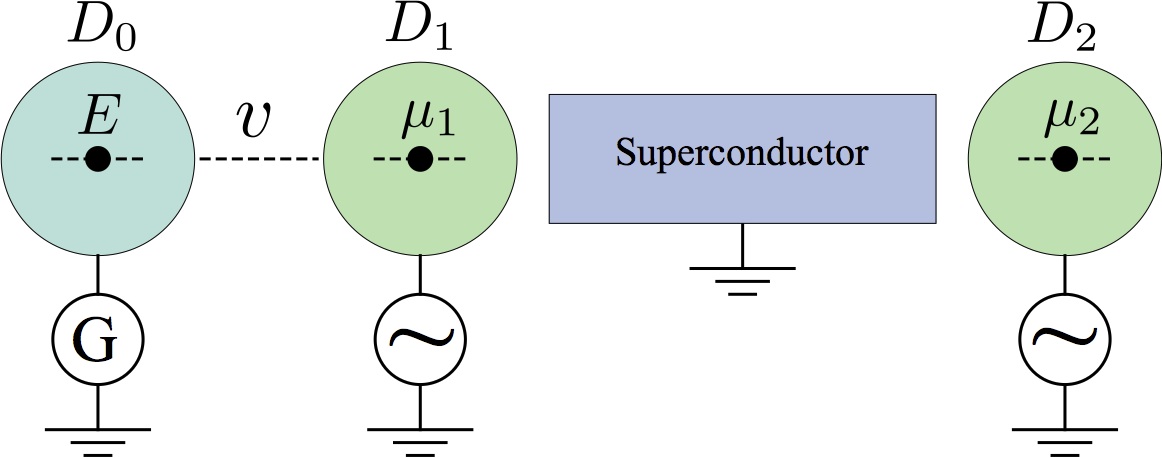
A quantum dots system for Floquet Majorana fermions.

Next, we proposed a way to realize and detect Floquet Majorana fermions in a simple system of two coupled quantum dots with exquisite tunability. This setup is a viable experimental proposal for two reasons: the tuning can be done entirely electronically; the Majorana fermions can be tested using a probe dot unambiguously. Although the topological stability is lost due to the small size of the system, the tunability of the system compensates this loss by making Majorana fermions easily accessible.

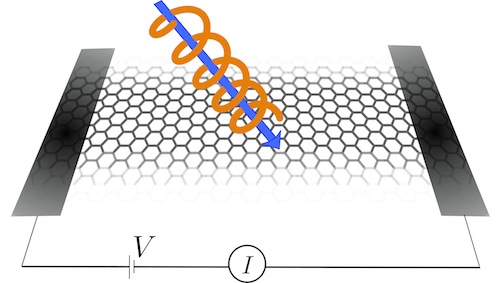
Graphene irradiated with circularly polarized laser.

In a separate project, my colleagues and I performed a theoretical and numerical study of graphene (an atomically thin sheet of graphite) under circularly polarized laser. This system was the original proposal for a Floquet topological phase. We found and characterized a series of distinct Floquet topological phases as the frequency and intensity of the laser is varied. At the transition between these phases, the system is critical with gapless bulk states. In a static situation this critical phase is manifested in a conductance \(\sigma(0)\) of the order \(e^2/h\). However, we showed that the dynamical nature of the topological phase can suppress this conductance due to an combined spatial and temporal symmetry of graphene. Interestingly, this symmetry is spoiled by disorder. Therefore, although one may naively expect disorder to be detrimental to transport, in this case it remarkably enhances the conductance by several orders of magnitude.

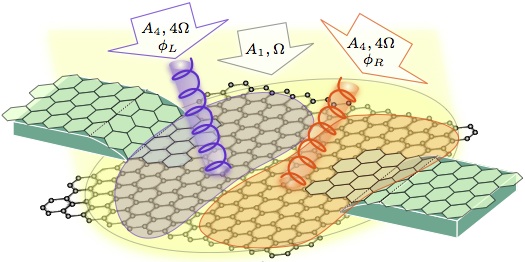
Laser-controlled valleytronics in graphene.

More recently, we have studied and proposed a novel way to realize valleytronic devices in two dimensional Dirac material, such as graphene or molybdenum disulfide, by optical engineering of the quasienergy band structure. By mixing and tuning the optical parameters of circularly-polarized lasers appropriately, the non-equilibrium steady state of electrons in different valleys can be differentiated to have unequal gaps. In particular, the gap at one valley can be closed while the gap at the other valley is still open. The conductance in this case is strongly valley-polarized. By opening and closing these gaps optically in different parts of the system, one may realize a valley switch. The valley-polarized conductance is protected against moderate impurity disorder and variations in optical parameters. This opens the way to engineering robust, novel electronic phases with light.

D. Dahan, E. Grosfeld, B. Seradjeh, Phys. Rev. B  102, 125142 (2020);
B. Seradjeh, M. Vennettilli, Phys. Rev. B  97, 075132 (2018);
M. Tanhayi Ahari, G. Ortiz, B. Seradjeh, Am. J. Phys.  84, 858 (2016);
D. Ariad, B. Seradjeh, E. Grosfeld, Phys. Rev. B  92, 035136 (2015);
C.-K. Lu, B. Seradjeh, Phys. Rev. B  89, 245448 (2014);
B. Seradjeh, M. Franz, Phys. Rev. Lett.  101, 146401 (2008).

Exhcnaging vortices in a chiral p-wave superconductor.

We have formulated an effective field theory of vortices in a two-dimensional spinless chiral p-wave superconductor. We devised a novel method of deriving the effective theory, which results in a \(\mathbb{U}(1)\times\mathbb{Z}_2\) effective gauge theory. The combined gauge transformation binds \(\mathbb{U}(1)\) and \(\mathbb{Z}_2\) defects so that the total transformation remains single-valued and manifestly preserves the the particle-hole symmetry of the action. The \(\mathbb{Z}_2\) gauge field introduces a complete Chern-Simons term in addition to a partial one associated with the \(\mathbb{U}(1)\) gauge field. Besides reproducing known dynamics of vortices ina superconductor, our theory predicts a universal Abelian exchange phase \(e^{i\pi/8}\) for two vortices in a superconductor, which is masked by an unscreened nonuniversal contribution in a neutral superfluid. This prediction is important for proposals to use Majorana fermions for universal quantum computation.

A. Rahmani, B. Seradjeh, M. Franz, Phys. Rev. B  96, 075158 (2017);
D. Dahan, M. Tanhayi Ahari, G. Ortiz, B. Seradjeh, E. Grosfeld, Phys. Rev. B  95, 201114(R) (2017);
B. Seradjeh, E. Grosfeld, Phys. Rev. B  83, 174521 (2011);
E. Grosfeld, B. Seradjeh, S. Vishveshwara, Phys. Rev. B  83, 104513 (2011).

Majorana modes in a layered topological superconductor.

A chiral p-wave superconductor permits a “half-quantum” vortex (HQV) that carries a flux \(h/4e\). The HQV can be thought of as a vortex in just one spin component. In the core of a HQV there is an electronic bound state pinned to the chemical potential, a so-called “zero mode.” Due to the special structure of the states in a superconductor, the particle realized by this zero mode is its own anti-particle, known as a Majorana fermion. This means that a doubly occupied zero mode is the same as one that is unoccupied, in contrast to regular fermions that obey Pauli's exclusion principle. In effect, a Majorana fermion is half of a regular fermion. HQVs are predicted to have non-Abelian fractional statistics. It is thought that Sr ₂RuO ₄ (SRO), a layered superconductor, has the right symmetry to host a chiral p-wave superconductor. A thin film of ³He-A is another example. More recently, the proximity-induced superconducting state of the surface of an STI has been shown to realize similar physics.

In a layered topological superconductor such as SRO, there are two Majorana fermions per layer in the core of a regular vortex (full-quantum with a flux \(h/2e\)), one for each spin components. Similarly, at the edge of the system there are two Majorana modes per layer. Since these Majorana modes can mix and pair into regular femions, the question arises whether there are any unpaired Majorana modes within this manifold. We have recently shown that indeed there exists a phase of the system where the answer is affirmative. Interestingly, in order to realize this phase, one must maintain a finite supercurrent through the layers, as shown in the figure. Unpaired Majorana modes exist for certain spin-orbit interactions as bound states at the two ends of a regular vortex.

Majorana fermions may be detected through the existence of zero modes by spectroscopic methods. But how can one detect the non-Abelian statistics of HQVs endowed by the core Majorana fermions?

Geometry of proposed Aharonov-Casher interferometer.

To answer this question, we proposed a two-path vortex interferometry experiment, based on the Aharonov-Casher effect. As shown in the figure, a superconducting annulus (yellow) is connected to leads (grey), and a supercurrent density \(\mathbf{j}_s\) is maintained across the sample. Vortices in the sample (red) feel a transverse Magnus force, similar in nature to the force that keeps the wings of an airplane afloat. Therefore, in the geometry shown in the figure, vortices flow from bottom to top and choose one of two paths (L and R) to circumvent the central hole. Charge \(Q\) on the central island (blue) is controlled by gates (not shown). A measurable voltage is induced across the leads by the vortex current \(\mathbf{J}_v\) via the Josephson relation. The quantum interference between the two paths can be observed as periodic oscillations in the voltage as \(Q\) varies with a period \(\Delta Q=2e\) for regular vortices and \(\Delta Q=4e\) for HQVs. When a HQV is stabilized at the hole (inducing currents shown by dashed arrows) we predict the interference pattern disappears due to non-Abelian statistics. In the case of SRO, we argue that under reasonable conditions this is true, remarkably, even if the itinerant vortices are regular vortices.

B. Seradjeh, Phys. Rev. B  86, 121101(R) (2012);
B. Seradjeh, Phys. Rev. B  85, 235146 (2012);
B. Seradjeh, J. E. Moore, M. Franz, Phys. Rev. Lett.  103, 066402 (2009);
B. Seradjeh, H. Weber, M. Franz, Phys. Rev. Lett.  101, 246404 (2008).

(a) Schematic of the thin film STI. (b) A vortex effectively realizes a 2D monopole.

A time reversal (T) invariant “strong” topological insulator (STI) supports topologically-protected, spin-filtered metallic surfaces with an odd number of crossing points in the surface energy bands. The energy of electronic states near the crossing point depends linearly on their momentum and therefore realize massless Dirac fermions. This is similar to the situation in graphene (a monatmic layer of graphite). But in graphene, like any other intrinsically two-dimensional (2D) system there is an even number of band crossings. The existence of such excitations leads to a number of exotic properties.

In a thin film of STI, when the chemical potential is tuned sufficiently near the surface band crossing point, an external bias makes the two parallel surfaces oppositely charged with electrons in one surface and holes in the other that have almost perfectly matching Fermi pockets, a condition known as nesting. An infinitesimal Coulomb interaction between the surfaces generates a coherent condensate of electron-hole bound states (excitons), very much like the coherent condensation of Cooper pairs in a superconductor. The condensate effectively joins the surfaces of the STI, yielding a toroidal topology and realizes a new topological state of matter. The topological character is manifested in the fractional quantum numbers of a vortex excitation in the condensate. The vortex realizes a 2D magnetic monopole between the surfaces, as depicted in the figure. The coupling of spin and momentum and an odd number of band crossings then ensure that a universal fractional charge of \(e/2\) is bound to the vortex, hence realizing the bound state of a magnetic monopole and electric charge (dyon). The fractional charge of the vortex is robust against weak T-invariant disorder and spatial variations of parameters through a mechanism first discussed by Witten in the context of certain topological QFTs. Recent advances in fabrication and sensitive measurements in a family of topological insulators promise experimental tests of these predictions in near future.

C. Weeks, G. Rosenberg, B. Seradjeh and M. Franz, Nature Phys.  3, 796 (2007);
G. Rosenberg, B. Seradjeh, C. Weeks and M. Franz, Phys. Rev. B  79, 205102 (2009).

Vortex lattice defects are anyons!

Could anyons exist in weakly-interacting and/or T-invariant systems? The answer has recently been shown to be affirmative. Notably, we proposed a weakly-interacting system comprising of a type-II superconducting film with an artificial array of pinning sites and a 2D electron gas (2DEG) in the integer quantum Hall regime with unit filling factor. A pinned lattice of superconducting vortices is formed in external magnetic field, each carrying half a flux quantum, \(\frac12\Phi_0=h/2e\). An excited state is found when a vortex is displaced from its pinning site to an interstitial position leaving a vacancy behind. This set up is sketched in the figure. Due to the incompressible nature of the integer quantum Hall state, a charge \(\pm e/2\) is accumulated at the center of the interstitial/vacancy in the 2DEG. This creates a bound state \((e/2,\Phi_0/2)\), a literal realization of Wilcsek's anyon model. Two such bound states behave as anyons with an exchange phase \(e^{i\pi/4}\). Moreover, we proposed an all-electric scheme for moving and possibly braiding these anyons. This scheme can be useful in manipulating anyons and be instrumental in quantum information processing.